平行四辺形 合同 証明 195355-平行四辺形 合同 証明 問��
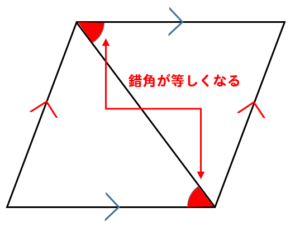
平行四辺形の性質を利用した証明 平行四辺形の内外にある三角形の合同を証明する問題もあるよ。 三角形の合同条件を改めて確認しておこう。 (1)3辺がそれぞれ等しい。 (2)2辺とその間の角が では平行四辺形の証明を順を追って説明しましょう。 使用する前提としては、1つの定義と4つの定理です。 つまり、平行四辺形なら、 向かい合う辺は平行であり、向かい合う辺は等し図形の証明問題を考えるときの3つの手順を示しておきます。 (1) 仮定と結論は何かをはっきりさせる (箇条書きにしておくとよい)。 (2) 仮定からわかることを図にかき入れてみる。 (3) 結論を導く
2
平行四辺形 合同 証明 問題
平行四辺形 合同 証明 問題- 「平行四辺形になる条件の5項目」 を!! この5項目中、 どれか1つでも証明できれば 、平行四辺形であることが証明できるんだったね? 平行四辺形の性質や、なる条件を忘れてしまっ平行四辺形の性質 証明の問題に、平行四辺形がでてくることがあります。 このとき、平行四辺形には以下の 4 4 つが成り立っていることは 暗黙の前提です。 証明なしで使って構いません。 ・ 2 2 組




中2 数学 四角形4 平行四辺形の証明2 17分 Youtube
こんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違 鈍角三角形1つだけ90°より大きい角を持つ三角形 鋭角三角形すべての角が90°より小さい角の三角形 これがルールなので見た目に騙されないでください! 合同の証明の仕方 もちろ 四辺形が平行四辺形であることを証明するには、これら5つの方法のいずれかを使用する必要があります。 反対側の両方のペアが平行であることを 証明 します。 反対側の両方のペアが
2 days ago 平行四辺形になるための条件 5つある「平行四辺形になるための条件」のうち, どれか1つでも条件が成り立つことを示せば, 平行四辺形であることを証明できます。 (1)2組の対辺がそれ※例1のような性質は「平行四辺形の2組の向かい合う辺はそれぞれ等しい」と表現されることもある. 問題 四角形 abcd について左欄の性質を証明するとき,どのような仮定からどのような結論を導 解き方 平行四辺形の性質を利用した証明問題のポイント 平行四辺形の性質は? AE=CFを示すには、三角形の合同を利用する ABE と CDF に着目しよう! 以下の3つがポイントだ! 平行
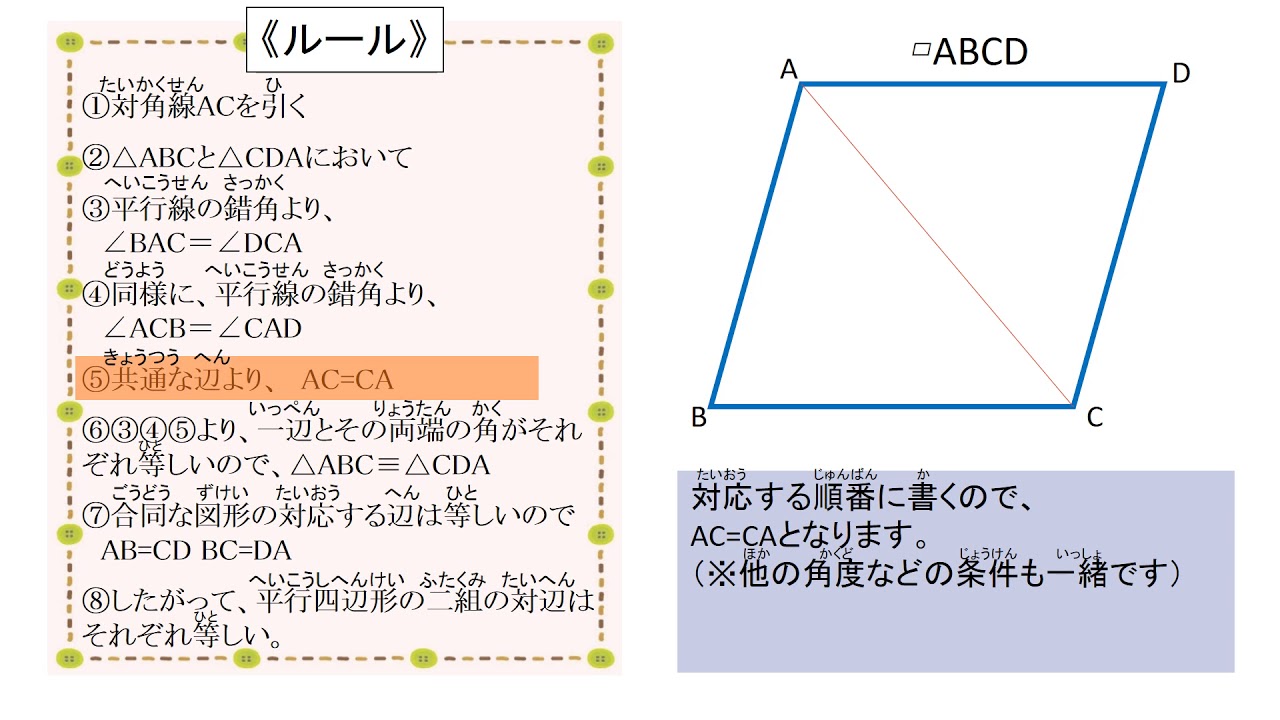
難問に挑戦しよう! 作成者 Bunryu Kamimura トピック 角, 円, 外接円, 合同, 作図, 幾何, 中線, 平行四辺形, ひし形, 回転, 正方形, 三角形 中学生でも解ける、大学生でも解けない難問。 ジオジェブ平行四辺形になる条件の証明 2 2組の向かいあう辺が、それぞれ等しい。 ABCと CDAで、 AB=CD 1 BC=DA 2 AC=CA (共通) 3 1,2,3より3辺がそれぞれ等しいので、 ABC≡ CDA よって 平行四辺形の証明問題 ここでは、ある図形が平行四辺形になるための条件と、証明問題の解き方を説明します。 平行四辺形になる条件 ある平面図形が平行四辺形であるための条件には



中学数学 平行四辺形の証明問題を徹底解説 数スタ



2
⑥ 、⑦より2組の対辺がそれぞれ等しいので四角形efghは平行四辺形となる。 (3) abeと cdfにおいて ab=cd (平行四辺形の対辺) ∠abe=∠cdf (ab//cdの錯角) ∠aeb=∠cfd=90°(垂線) よって直角三角形の斜この平行四辺形になる5つの条件については、正確に暗記し、問題場面に応じて"活用できる"ことが 重要である。 2 ※図の表し方は同じ意味ならよい。中学数学平行四辺形になることの証明・その2 三角形の合同の証明の利用 四角形 ABCD A B C D が平行四辺形であることを示すために、 辺の長さ、角の大きさが等しいことを示したいときがあ
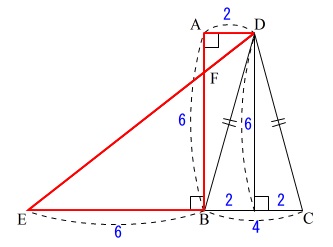



18年大阪府公立高校入試数学a問題問4の図形問題の解説



三角形の合同 平行四辺形 苦手な数学を簡単に
平行四辺形を利用した中点連結定理の証明 証明② 平行四辺形の性質を利用 手順: 1 平行四辺形の性質である「対角線がそれぞれの中点で交わる」を利用して、 abcの辺caを対角線 中学全学年 証明の書き方の説明です。 定義と定理の扱い方は、関連ノートを見てください 三角形と四角形 数学証明 平行四辺形 定義 定理 三角形の合同 マジックの勉強部屋 この著者の四角形は、次の5つのどれかが成り立てば平行四辺形になります。 これを 平行四辺形になるための5つの条件 といいます。 ネコくんが喋っているように、④⑤の条件は証明でよく使われるため、他よ



平行四辺形を使った証明 On Vimeo




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット
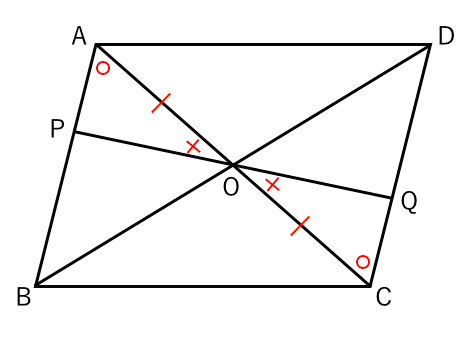
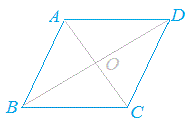
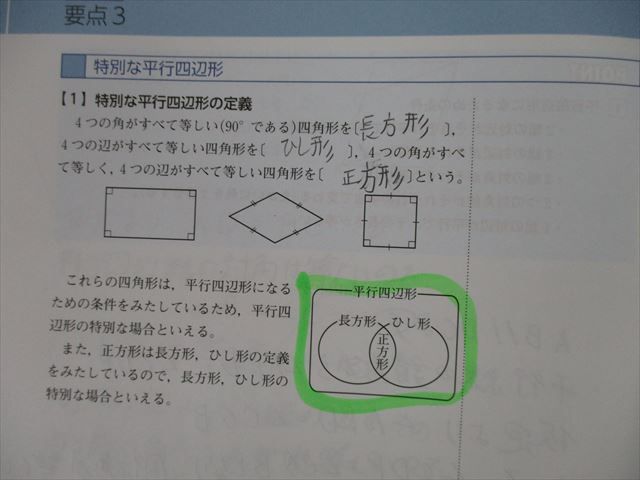
平行四辺形 平行四辺形の定義 2組の対辺がそれぞれ平行な四角形 平行四辺形の定義からつぎの性質を導くことができる 2組の対辺はそれぞれ等しい。 >>証明 2組の対角はそれぞれ等しい。 >>証明 合同な図形の性質 ・合同な図形では、 対応する線分の長さや角の大きさはそれぞれ等しい 。 ・ 「≡ ≡ 」 は合同を表す記号である。 この記号を使うときは、対応する頂点の順に並べる 平行四辺形の証明実践問題 次の図の平行四辺形ABCDの辺AD上に点EをCE=CDとなるようにとり、点AとC、B、Eをそれぞれ結んだ場合を表しているとき ACD≡ BECであることを証明せ



三角形の合同 平行四辺形 苦手な数学を簡単に



証明の進め方 平行四辺形の証明問題
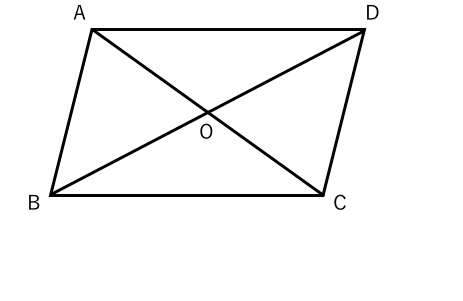
Z証明 { aomと conにおいて 平行線の錯角は等しいからad//bcより ∠mao=∠nco・・・① 平行四辺形の対角線はそれぞれの中点で交わるから ao=co・・・② 対頂角は等しいから ∠aom=∠con・・・③ 平行四辺形の性質その1:対辺の長さが等しい 対辺とは 「向かい合う辺」 のことです。 証明は対角線によって、平行四辺形を2つの三角形に分け、その三角形の合同を示すことでできま平行四辺形 ⇒ ( ならば) 1組が平行でかつ等しい も当然〇となりますね! では本題、その逆は? ⑤'四角形abcdの1組の対辺が平行でかつ等しい ⇒ ( ならば) 平行四辺形? (証明) 対角線ac、bdを引



平行四辺形の性質の利用2




中学数学 平行四辺形の証明問題を徹底解説 数スタ
今回は中2数学で学ぶ、平行四辺形になる条件について勉強したいと思います。 平行四辺形になる条件 2組の対辺がそれぞれ平行である 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ 中学数学:中2合同の証明16 年8月6日 こんにちは。 今回は中2の合同の証明です。 正三角形が組み合わさっています。 最後は平行四辺形の証明が入っています。 履修済みの方平行四辺形になる条件 平行四辺形になる条件 四角形は、次の性質のどれかをもつと、平行四辺形である。 1 2組の向かいあう辺が、それぞれ平行である。 ( 定義 ) 2 2組の向かいあう辺が、それぞ
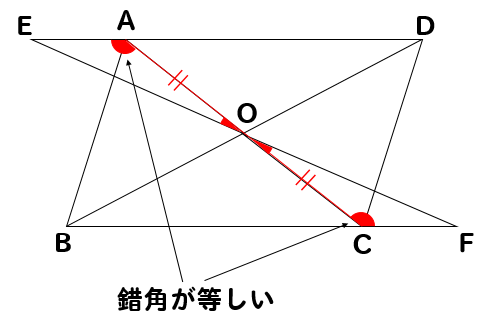



中学数学 平行四辺形の証明問題を徹底解説 数スタ




S4sr Mhul5seum
平行四辺形の証明のまとめ ・平行四辺形の証明で よく使う流れ 「垂線」という「仮定」から 2直線の「錯角」が等しい 2直線が「平行」であることを証明します 「平行四辺形」とい平行四辺形の合同条件を教えてください! (証明) 0 回答 ベストアンサー ゆず 🌸 4年以上前 平行四辺形の合同条件 ①2組の対辺はそれぞれ平行である ②2組の対辺はそれぞれ等しい ③2組の対角はそ
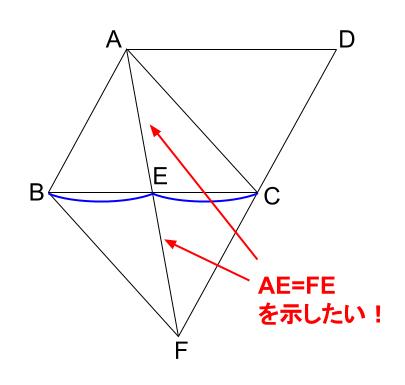



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su



2
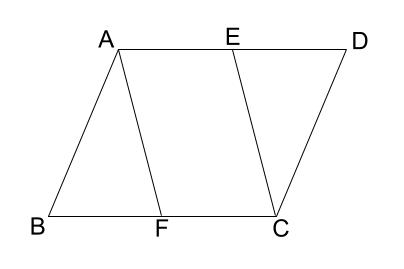



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




平行四辺形の証明 ズバリ解き方はこれ 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




Math 平行四辺形 平行四辺形になることの証明 働きアリ



証明の問題です 平行四辺形abcdにおいて対角線bdが角bを Yahoo 知恵袋




中学校数学 証明のコツ 年01月
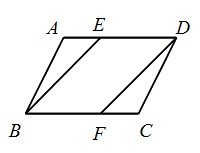



Math 平行四辺形 平行四辺形になることの証明 働きアリ




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット




中学数学 平行四辺形の証明問題を徹底解説 数スタ
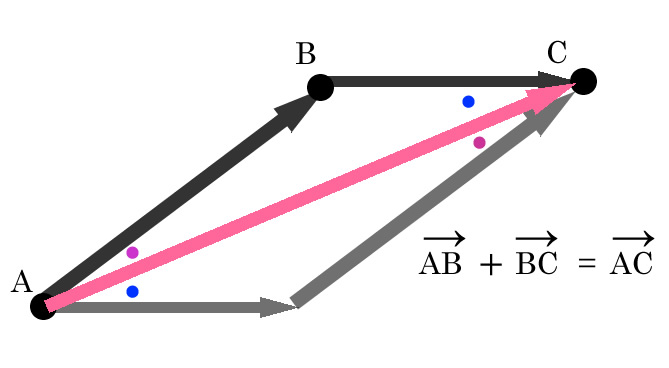



ベクトルのきほん 優技録
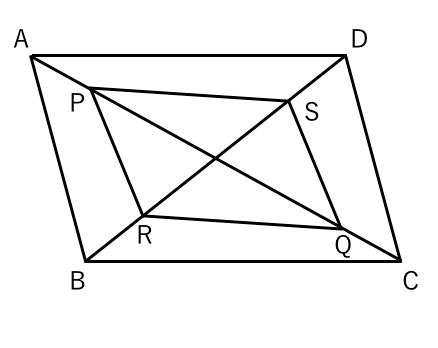



平行四辺形であることを証明する 苦手な数学を簡単に
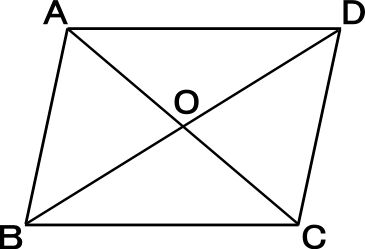



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同
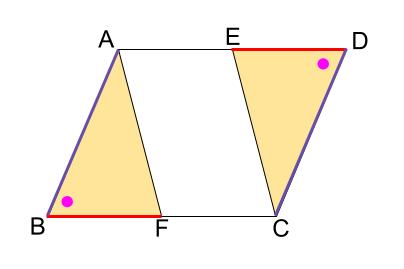



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su
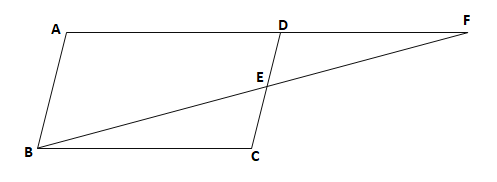



中2数学 平行四辺形の証明の定期テスト対策予想問題 デルココ




中学校数学 証明のコツ 年01月



2



平行四辺形の性質の利用2




中学数学 平行四辺形の証明問題を徹底解説 数スタ
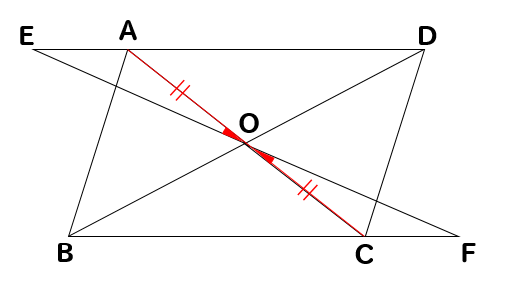



中学数学 平行四辺形の証明問題を徹底解説 数スタ



平行四辺形になるための証明3




ジロリアン Aglssbty Twitter
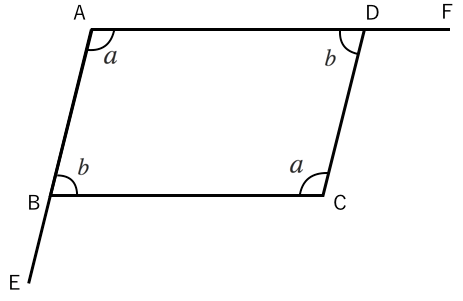



合同な三角形 平行四辺形で証明 苦手な数学を簡単に




中2 数学 四角形4 平行四辺形の証明2 17分 Youtube



Q Tbn And9gcryyacyufsamtoaasqp93zympl8ermiwy3q78uuue Rv11d0xjf5yif Usqp Cau
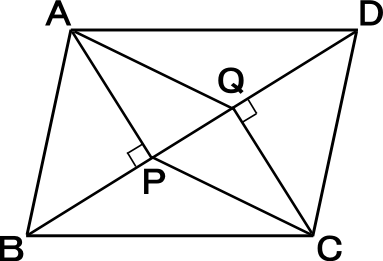



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同




中学数学 平行四辺形の証明問題を徹底解説 数スタ



Q Tbn And9gcqm7havqkg D4tj48v78iidwpxzhxl9epyxpu0v9h6sb Mru Ndrt6i Usqp Cau




フローチャート フロー図 書き方 まとめ 基本のキ Rakus Developers Blog ラクス エンジニアブログ




中2数学 平行四辺形の証明 例題編 映像授業のtry It トライイット
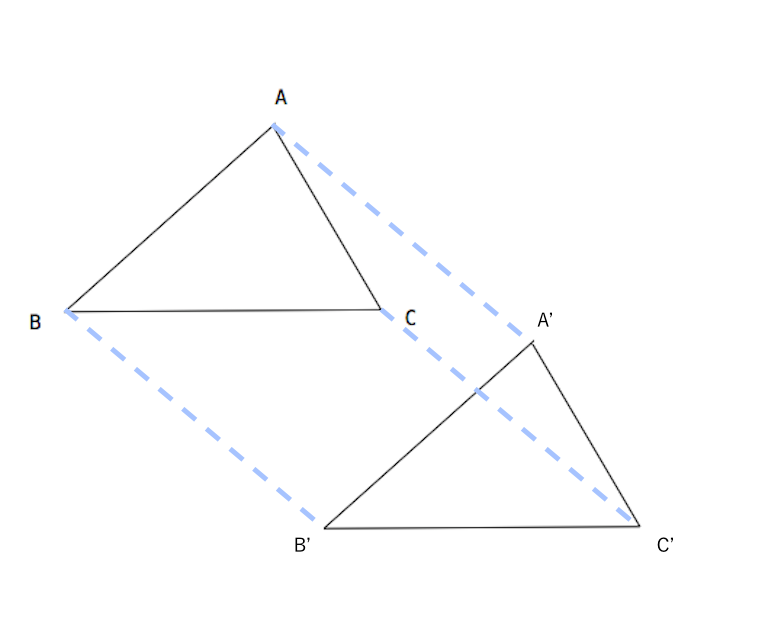



合同な三角形 平行四辺形で証明 苦手な数学を簡単に



平行四辺形の証明を教えてください 平行四辺形の証明が分かりません Yahoo 知恵袋



合同な三角形 平行四辺形で証明 苦手な数学を簡単に




数学 中2 74 平行四辺形になる条件 Youtube



平行四辺形の向かい合う角が等しいことの証明 Ad Ab Dcの Yahoo 知恵袋
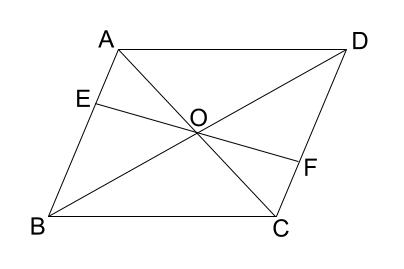



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su



オープニング大セール Rf92 041 L2d 計25冊 等 国語 英語 数学 理科 社会 地理 歴史 公民 要点ブック 定期テスト攻略ワーク Zstudy 中1 3 Z会 高校受験 Labelians Fr




平行四辺形の証明 ズバリ解き方はこれ 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



Q Tbn And9gcqphs9hw5adpyphvpdh9dspareojwrd1ubr1z2nioxzp1k719peaclm Usqp Cau



相似の証明をしてください M M1 平行四辺形abcdの辺の Yahoo 知恵袋



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形 中学数学で遊ぶ 身勝手な主張



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形であることを証明する 苦手な数学を簡単に



合同な三角形 平行四辺形で証明 苦手な数学を簡単に
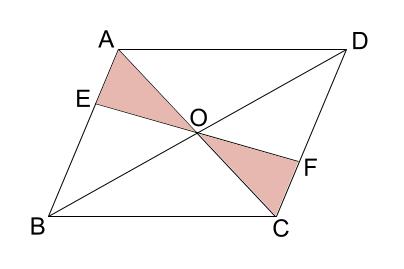



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su



平行四辺形の向かい合う角が等しいことの証明 Ad Ab Dcの Yahoo 知恵袋



Math 平行四辺形 平行四辺形になることの証明 働きアリ




中学数学 平行四辺形の証明問題を徹底解説 数スタ
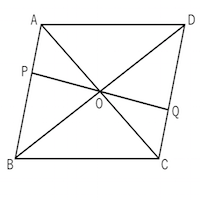



三角形の合同 平行四辺形 苦手な数学を簡単に




フローチャート フロー図 書き方 まとめ 基本のキ Rakus Developers Blog ラクス エンジニアブログ



Tossランド 平行四辺形の性質
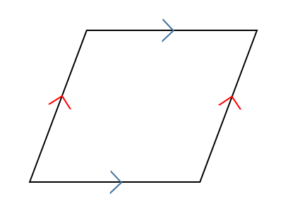



中学数学 平行四辺形の証明問題を徹底解説 数スタ



2




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット




平行四辺形と証明 Youtube



ピタゴラスの定理の簡単な証明方法ありますか Quora
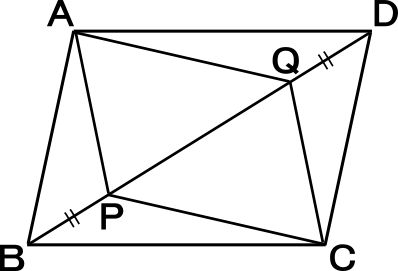



中学2年数学練習問題 平行四辺形になる条件と証明方法 図形と合同



2




S4sr Mhul5seum



平行四辺形になるための証明1




中2数学 平行四辺形の性質の利用 練習編 映像授業のtry It トライイット
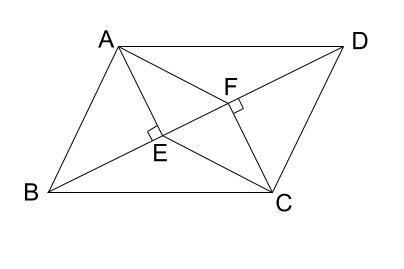



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形になるための条件 Youtube



平行四辺形になることの証明 On Vimeo



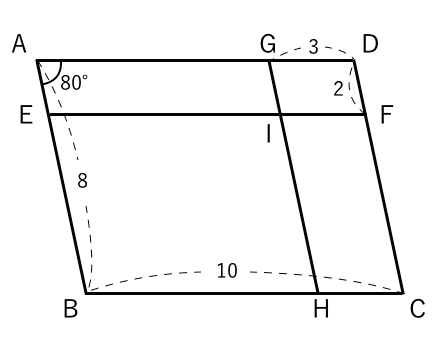
至急 数学証明平行四辺形の折り目の問題です どなたかご教示お願い致し Yahoo 知恵袋




フローチャート フロー図 書き方 まとめ 基本のキ Rakus Developers Blog ラクス エンジニアブログ




平行四辺形 中学数学で遊ぶ 身勝手な主張




中学数学 平行四辺形の証明問題を徹底解説 数スタ
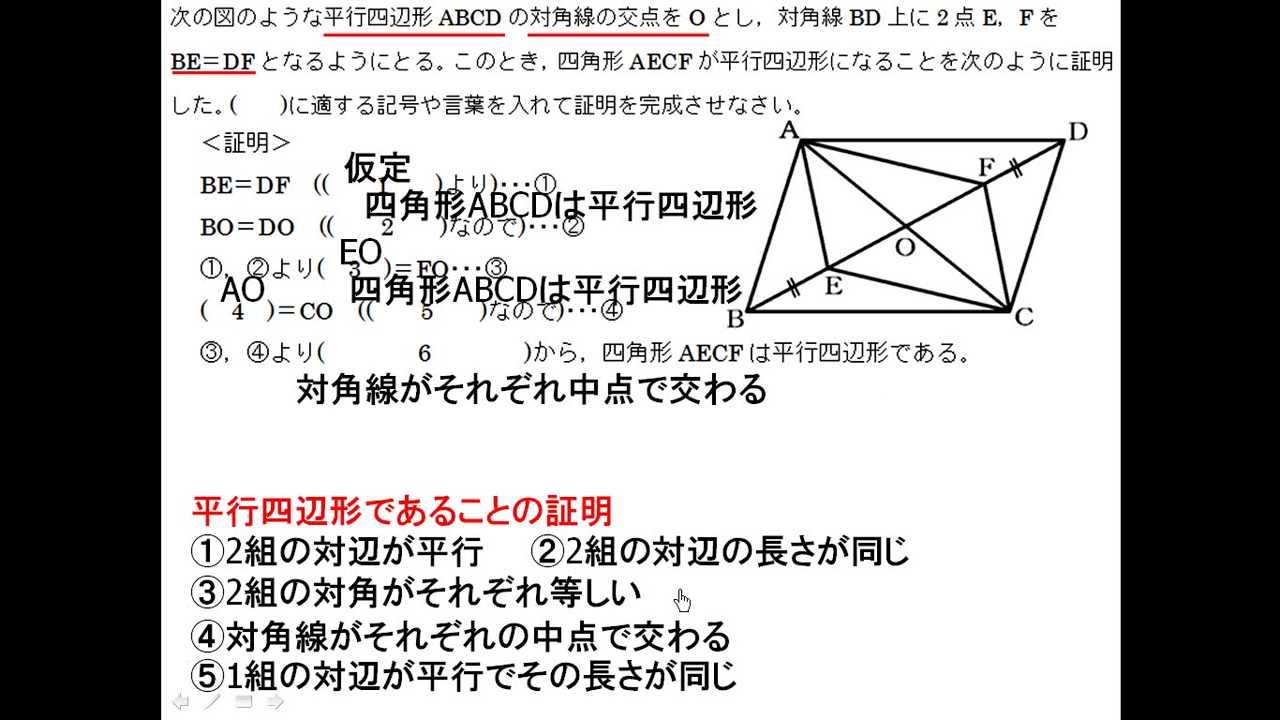



中2 数学 5 3 平行四辺形の証明 Youtube



平行四辺形になるための証明1



相似の証明をしてください M M1 平行四辺形abcdの辺の Yahoo 知恵袋



2




勉強しよう数学解答集 余弦定理に類似した中線の式と方ベきの定理の解答




中2数学 平行四辺形の証明 練習編 映像授業のtry It トライイット



Math 平行四辺形 平行四辺形になることの証明 働きアリ The 2nd
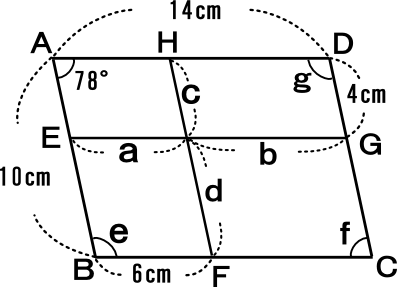



中学2年数学練習問題 図形と合同 平行四辺形の性質と証明問題



中2 平行四辺形の性質の証明1 対辺 日本語版 Youtube




中学校数学 証明のコツ 年01月



ジロリアン Aglssbty Twitter



中2数学 平行四辺形の証明のポイントと練習問題 Examee



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン



中学数学 平行四辺形の証明問題を徹底解説 数スタ



Q Tbn And9gcthx6w0o G Vblx8a Ajrpmheahn7ckfrvjct0fjf8o7r Dkwoozugm Usqp Cau




中学校数学 証明のコツ 年01月
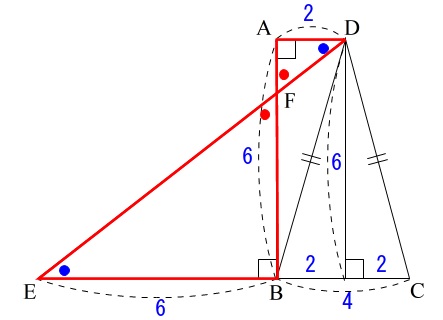



18年大阪府公立高校入試数学a問題問4の図形問題の解説




S4sr Mhul5seum




企業等に蓄積されたデータを分析するための処理機能の提案
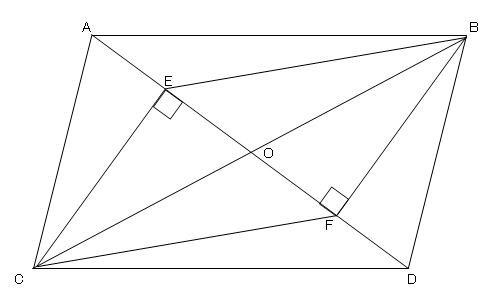



平行四辺形の証明 4 ネット塾




三角形と四角形 平行四辺形であることの証明の仕方 中学数学 定期テスト対策サイト




中学校数学 証明のコツ 年01月
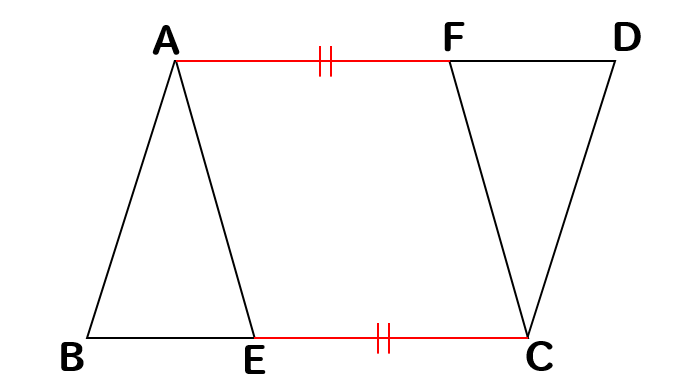



中学数学 平行四辺形の証明問題を徹底解説 数スタ
コメント
コメントを投稿